|
We are still assessing, it seems, a number of business and supply chain questions coming out of this “great recession.”
One of those surely is going to involve still more analysis – and eventual action – relative to “insourcing” versus outsourcing.
Today’s column is in fact going to be one of a brief series (spread over the next couple of months) on this topic.
There is simply no question, from what I have read lately and many of the conversations I have had with SCM execs – that this economic mess has led to an acceleration of CEO interest in continuing to move their companies to more variable cost structures – and supply chain is clearly in the cross hairs of that analysis.
While I have been planning these columns for awhile, the specific trigger this week was listening to the Hershey Foods Q4 earnings call. As you may or may not know, Hershey announced in 2007 a “global supply chain transformation” program that – traumatic to many – eventually included the outsourcing for the first time of chocolate production, always before considered a “core competency.” Not so much anymore, it seems.
Gilmore Says: |
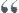 Core,” says Moore, is “any aspect of a company’s operation that creates differentiation leading to customer preference during a purchase decision. Core,” says Moore, is “any aspect of a company’s operation that creates differentiation leading to customer preference during a purchase decision. 

Click Here to See
Reader Feedback
|
It looks like a good move, as, despite some pretty significant costs for closing down plants, Hershey’s CFO told analysts that the move was delivering big savings already, with many more hundreds of millions to come over the next decade.
Most of us are familiar with a common framework for insource versus outsource analysis, which uses a typical 2 x 2 matrix (see image below; full size available by clicking link below it). On one dimension is the level of importance of a supply chain function or process to an organization (high or low); on the other dimension is the organization’s competence or effectiveness at the function/process (high or low).
High/high combos are clear “keepers;” low-low are clear outsourcing candidates. The high-low/low high combinations require more nuanced analysis, with some bias towards outsourcing functions of high importance and low competence, as it is likely you can find an outsourcer that can in fact do this important thing well.
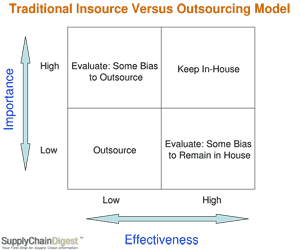
click for larger image
But there is another riff on this topic that is equally fascinating and in many ways better. It comes from Geoffrey Moore, the well-known business writer and thinker, who got on the map from my view with his book Crossing the Chasm, followed by a string of other business best sellers.
I’ve had the pleasure of meeting Moore a couple of times, and he is both very smart and a very nice guy. At one event where I saw him present, in fact, we had a follow up conversation on material from his book Dealing with Darwin, which is what my discussion is about here.
In that book, Moore focuses on the absolute business need for continuous innovation. I will note he is largely associated with the high tech industry, where innovation is clearly the lifeblood of success, but that’s now the case in almost every industry. CEO after CEO is saying it. As just one example, I had a recent discussion with a VP of Logistics at a private label consumer packaged goods manufacturer who told me retailers are increasingly pressing his company for innovative new products, not just knock-offs of branded goods.
I can’t hope to do full justice to all Moore’s thinking here, but on this particular point, he says simply that more corporate resources must be focused on innovation, and that in the end comes from outsourcing what isn’t “core” and refocusing those resources on innovation activity.
From this then comes his rather well known model of “core” versus “context.”
What is “core?” Interesting to me, “core,” says Moore, is “any aspect of a company’s operation that creates differentiation leading to customer preference during a purchase decision.”
“Context,” conversely, is basically “everything else.” Moore says that this context work can be important - and even highly valued - but that does not mean it contributes to customer differentiation.
So, his model of what to keep and what to outsource is a little different, as shown in graphic below.
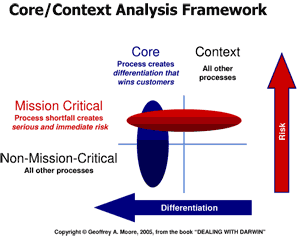
click for larger image
One different and commendable aspect of Moore’s approach is that he says you must re-deploy employees affected by the outsourcing move back into more innovative or core processes. Otherwise, he told me not long after this book came out in 2005, employees will (smartly, for their own good) strongly resist making outsourcing programs work. His vision is really one of a virtuous cycle that leads to continuous innovation.
He also makes another important point. What is “core” today is “context” tomorrow. In other words, processes tend to become more commoditized over time – maybe even rapidly.
The logic makes a lot of sense. But there are issues, I think.
1. How many companies really ever “re-deploy” employees (blue or white collar) impacted by supply chain outsourcing decision?
2. The decisions are often permanent – in other words, take something like demand planning or transportation management. Is it not possible that what might be context today could re-emerge as core later as practices and technologies change? But once it’s gone, can you ever really bring it back?
3. Supply chain cost is a tricky one: Right now obviously - but really a continuing trend even before the recession – “price” is one heck of a factor in “customer preference.” Look no further than the strong growth of lower priced private label goods in 2009. So how is cost advantage – now, or in the future – really considered in this model? The Chinese are winning product markets in part through “cost innovation.”
So in the end I am note sure. There is much logic in Moore’s model, but not perfect logic. The supply chain is a real conundrum – for example, total cost might even be higher in an outsourced model in good times, but much lower in bad times by having a more variable cost structure. My friend and SCDigest contributor Gene Tyndall says you can outsource the execution but must maintain the management, so you can bring it back when it makes sense - but is this really what most companies really do?
I don’t fully know, and the answer as usual is certainly “it depends.” But the "core versus context" question is getting still more steam in corporations worldwide – and SCM professionals better be prepared to defend their case.
What are your thoughts on supply chain outsourcing? What do you think of the "core versus context' model? Let us know your thoughts at the Feedback button below.
|